10er-Übergänge - Kein Problem!
Auf meinen speziellen Plus- und Minus-Rechentafel werden 10er-Übergänge sichtbar.
Stellenübergänge bei Additions- und Subtraktionsaufgaben verstehen lernen
Die Plus- und Minus-Rechentafeln (ZR 20 und ZR 100) bestehen jeweils aus 3 Mengenfeldern. Im unteren Bereich befinden sich die Teilmengenfelder
Teil 1 und Teil 2. Darüber liegt als großes Feld das Feld für das Ganze bzw. die Gesamtmenge oder bei Minusaufgaben die Ausgangsmenge.
Aus dem Set für den Zahlenraum bis 20
20er-Plus-Rechentafel
20er-Minus-Rechentafel
Aus dem Set für den Zahlenraum bis 100
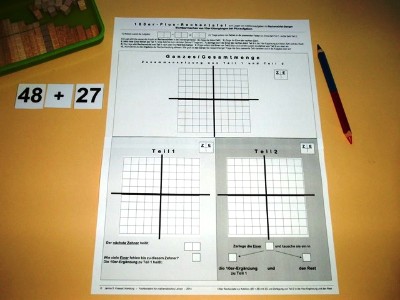
100er-Plus-Rechentafel
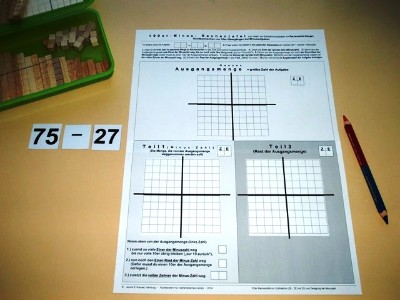
100er-Minus-Rechentafel
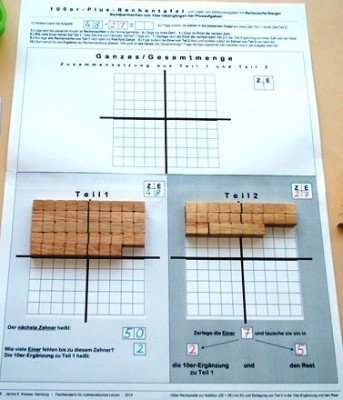
Beim Legen von Additionsaufgaben mit den Rechenwürfeln auf den Plus-Rechentafeln wird deutlich, dass das Aufgabenergebnis die
Gesamtmenge (das Ganze) ist, die aus 2 Teilmengen (Teil1 = 1. Summand und Teil 2 = 2. Summand) zusammengesetzt wird.
Aufgabe: 8 + 7
Aufgabe: 48 + 27
Beim Legen von Subtraktionsaufgaben mit den Rechenwürfeln auf den Minus-Rechentafeln erleben die Kinder, dass bei diesen Aufgaben die größte Zahl die Ausgangsmenge, das Ganze, ist, von der ein Teil, die Minuszahl, weggenommen wird, und als Aufgabenergebnis eine zweite Teilmenge übrig bleibt.
Entsprechend der größten Zahl wird also eine Menge von Rechenwürfeln als Ausgangsmenge oben in das Feld für das Ganze gelegt. Von dieser Menge wird eine der Minuszahl entsprechende Teilmenge weggenommen. Die übrigbleibende zweite Teilmenge ist das Aufgabenergebnis.
Aufgabe: 15 - 7 Aufgabe: 75 - 27
Nach der Erarbeitung der Aufgabe auf der Plus- oder Minus-Rechentafeln trägt der Schüler zur festigenden Wiederholung die Aufgabenlösung nun auf der "Tafel zum Sichtbarmachen der Rechenschritte bei Plus- und Minus-Aufgaben mit ZÜ im ZR bis 20" ein.
Bei der Erarbeitung der Aufgabenlösung mit Rechenwürfeln auf einer Rechentafel im Zuge einer Rechenhandlung lernt der Schüler, was bei Additions- und Subtraktionsaufgaben mengenmäßig vor sich geht. Er kann dabei sehen, was bei Aufgaben mit Stellenübergängen mit den einzelnen Mengen passiert.
Werden die einzelnen Schritte der Rechenhandlung begleitend immer auch mit Zahlen notiert, bilden sich beim Schüler Vorstellungsbilder dazu, was beim Lösen einer Rechenaufgabe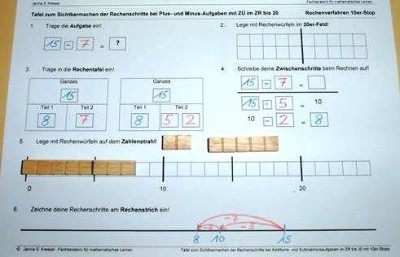 
eigentlich passiert. Diese Vorstellungsbilder ermöglichen es später, wenn kein Material mehr vorhanden ist, dass die Aufgabenlösung auch ganz ohne Material zeichnerisch wiedergegeben werden kann.
Hat ein Schüler den intermodalen Wechsel von Rechenhandlung, Zeichnung und abstraktem Rechnen erlernt, kann er später seine Arbeitsergebnisse auch stets ohne konkretes Material allein durch Skizzieren der vorgestellten Rechenhandlung selbstständig auf Richtigkeit hin überprüfen.
Auf dieser Rechentafel wird die Rechnung zum Beispiel durch Sprünge auf dem Rechenstrich eingezeichnet
Aber auch die Rechenhandlungen mit den Rechenwürfeln lassen sich auf kleinen selbst gezeichneten Rechentafeln einfach skizzieren.
Auf den folgenden 2 Info-Bögen ist dargestellt, wie dies am besten erfolgen sollte.
Zuerst müssen dafür Abmachungen getroffen werden, was für ein Zeichen für einen Einer, einen Zehner, und einen Hunderter gezeichnet wird. Auf den Info-Bögen hat man verabredet: Ein Punkt repräsentiert einen Einer, ein Strich eine Zehner-Stange, ein halber Strich mit einem kleinen Häkchen (5er-Markierung) einen Fünfer-Stab und ein Quadrat ein Hunderter-Platte
.
Auf den beiden Info-Bögen "Additions- und Subtraktionsaufgaben mit Stellenübergängen auf 5 verschiedene Weise lösen" (je 2 Bögen für den ZR 100 und den ZR 9.999) für Lehrer und Eltern wird folgendes dargestellt:
1.) Aufgabe mit Dienes Rechenwürfeln auf der 100er-Plus- bzw. 100er-Minus-Rechentafel oder im ZR 9.999
auf dem großen Rechenbrett legen
2.) Aufgabe über Halbschriftliches Rechnen lösen
3.) Rechengeschichte zur Aufgabe erzählen
4.) Aufgabenlösung zeichnen
5.) Aufgabe durch Schriftliches Rechnen lösen und dazu sprechen
Auf den Arbeitsblättern "Rechne mit 10er-Stopp" wird eine Aufgabe jeweils in
4-facher Weise dargestellt:
1.) Als Kurzform mit der notwendigen Zerlegung des 2. Summanden
2.) In der halbschriftlicher Rechenweise
3.) Auf einer kleinen Rechentafel
4.) Einzeichnen der Rechenschritte auf dem Rechenstrich
Die Info-Blätter "Die Tripelstruktur macht Lückenaufgaben verständlich" zeigen die Bezüge, dass z u 3 Zahlen (einem Zahlentripel) immer 4 Aufgaben (2 Plus- und 2 Minus-Aufgaben) gehören .
Die Rechentafeln verdeutlichen dieses Teil - Teil - Ganzes-Prinzip in besonders anschaulicher Weise.
Wenn der Schüler verstanden hat, dass er aus den 3 Zahlen einer Plus-Aufgabe auch die Tausch- und die Umkehraufgaben bilden kann und umgekehrt ( so z. B.: 7 + 8 = 15 die Tauschaufgabe 8 + 7 = 15 und die Umkehraufgaben 15 - 7 = 8 und 15 - 8 = 7), so wird es ihm mit Hilfe der Rechentafel möglich, alle Arten von Lückenaufgaben zu lösen.
Der Schüler trägt die jeweils gegebenen zwei Zahlen an die zugehörigen Stellen in der Rechentafel ein und kann daraus dann entnehmen, ob die nicht bekannte Ergebniszahl durch Zusammenschieben der beiden gegebenen Teilmengen (bei einer Plusaufgabe) oder durch das Herunterschieben einer Teilmenge von der oberen Ausgangsmenge (bei einer Minusaufgabe) zu finden ist.
Diese Info-Blätter können erst einmal eine ganze Weile mit auf dem Tisch liegen, und der Schüler versucht, für seine zu lösende Aufgabe ein Pendant auf dem Bogen zu finden. Hat er erkannt, welches Feld in der Rechentafel der gesuchten Zahl in seiner zu lösenden Aufgaben entspricht, kann er dem Info-Blatt auch entnehmen, wie er nun vorgehen muss. Für jede Aufgabenlösung stehen immer 2 Rechenarten zur Verfügung.
.
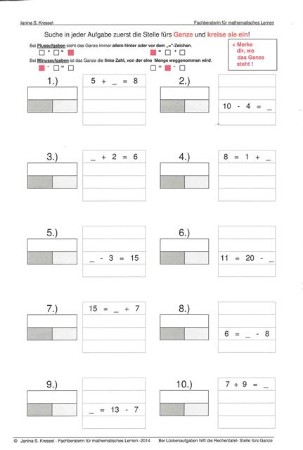
Mit dem folgenden AB "Suche in jeder Aufgabe zuerst die Stelle fürs Ganze und kreise sie ein!" soll der Schüler zunächst eine Vorstellung davon gewinnen, ob das Ganze in der Aufgabe schon bekannt ist.
.
Als nächstes werden die beiden angegebenen Zahlen in die entsprechenden Felder der kleinen Rechentafel eingetragen.
Jetzt kann der Schüler die fehlende dritte Zahl durch konkrete Rechenhandlungen mit Rechenwürfeln auf seiner Rechentafel oder auch über eine Rechenhandlung in der Vorstellung finden.
Wenn alle drei Zahlen des Zahlentripels bekannt sind, müssen noch die anderen
3 Aufgaben gebildet und in das Aufgabenkästchen eingetragen werden, sodass zu jedem Zahlentripel 4 Aufgaben vorhanden sind.
Das Besondere dieser speziellen Rechentafeln besteht darin, dass sowohl bei der Plus- als auch bei der Minus-Rechentafel in jeweils einem Teilmengenfeld die Raster für Zerlegungen schon vorgegeben sind. Bei den Rechenhandlungen mit Rechenwürfeln auf diesen speziell strukturierten Rechentafeln werden mit Hilfe dieser Raster 10er-Übergänge sichtbar.
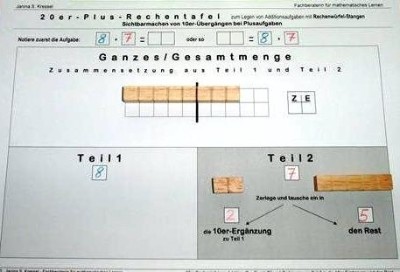
Für Plusaufgaben mit 10er-Übergängen ist im 2. Teilmengenfeld
(2. Summand) ein solches Raster vorhanden, mit dem eine Aufteilung dieser Teilmenge in die 10er-Ergänzung zu Teil 1 und den Rest verdeutlicht wird.
Indem die 1. Teilmenge nach oben in das 20er-Raster des Feldes für die Gesamtmenge geschoben wird, ist dort die fehlende Ergänzung, bis der 10er voll ist, auf Grund des unterlegten Rasters visuell sofort ersichtlich.
(Hier: Zum vollen 10er fehlt ein 2er.)
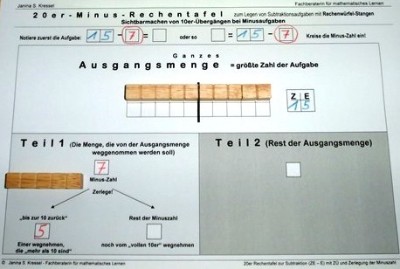
Für Minusaufgaben mit 10er-Übergang ist im 1. Teilmengenfeld der Minuszahl ein solches Raster vorhanden, mit dem die Minuszahl zerlegt wird.
Das geschieht dadurch, dass von der Ausgangsmenge oben zuerst nur die Einer weggenommen werden, die mehr als 10 sind (also das, was im zweiten 10er-Raster liegt - nach der Strategie "bis zur 10 zurück"); danach muss der volle 10er zerlegt werden, um den Rest der Minuszahl davon noch wegnehmen zu können. (Hier:"Wenn ein 7er weggenommen werden soll und ein 5er schon heruntergeholt wurde, so muss der 10er so zerlegt werden, dass der zweite Teil des 7ers, ein 2er, noch weggenommen werden kann.")
Das große Rechenbrett zur Darstellung von Additions- und Subtraktionsaufgaben im ZR bis 9.999 ist anders aufgebaut als die Rechentafeln.
Hier werden die Mengen genauso untereinander angeordnet, wie man beim Schriftlichen Rechnen vorgeht.
Hier z. B. bei der Minus-Aufgabe 600 - 136 legt der Schüler zuerst die Ausgangsmenge in E-, Z-, und Hunderter-Fächer dir oberste Reihe.
Die der Minuszahl entsprechenden Mengen werden sodann davon weggenommen und in die mittlere Reihe gelegt,. Der übrig bleibende Rest gelangt zuletzt in die unterste Reihe, unter dem roten Strich, in die Ergebnisreihe.
Die nebenstehende Abbildung zeigt das Vorgehen (Einwechseln der Hunderter und Zehner, um Einer zu bekommen) bei einem doppelten Stellenübergang.
Die Handlungserklärungen, die genaue Notation und auch die Sprechweise dazu werden in der Anleitung detailliert erklärt.
Ich habe 3 Sets mit Material zum Verstehen-Lernen der 10er- und Stellenübergänge zusammengestellt.
Jedes Set enthält neben den Rechentafeln für den ZR 20, den ZR 100 sowie dem großen Rechenbrett für den ZR bis 9999 eine genaue Anleitung mit Fotodokumentation aller einzelnen Vorgehensschritte.
Als Zusatzmaterialien werden Rechenwürfel sowie ein abwischbarer Folienstift benötigt.
Folgende Sets sind einzeln erhältlich:
Set Zahlenraum bis 20
- 10-seitige Anleitung mit farbigen Darstellungen
- 3 laminierte Rechentafeln zum Beschreiben
- 2 Infos zu Lückenaufgaben
- 1 Arbeitsblatt
(Nicht enthalten, aber notwendig:
Rechenwürfel- und Anzahlstangen-Set)
Bestellformular
Set Zahlenraum bis 100
- 13-seitige Anleitung mit farbigen Darstellungen
- 2 laminierte Rechentafeln zum Beschreiben
- 1 Info zu Lückenaufgaben
- 1 Arbeitsblatt "3 Zahlen - 4 Aufgaben"
- 6 Arbeitsblätter "Rechnen mit 10er-Stopp"
- 2 Infos "Additions- und Subtraktionsaufgaben
mit Stellenübergängen auf 5 verschiedene Weise lösen"
(Nicht enthalten, aber notwendig:
Rechenwürfel- und Anzahlstangen-Set)
Bestellformular
Set Zahlenraum 1.999 (auch bis 9.999)
- 10-seitige Anleitung mit farbigen Darstellungen
- großes Rechenbrett
- 2 Infos "Additions- und Subtraktionsaufgaben
mit Stellenübergängen auf 5 verschiedene Weise lösen"
Gearbeitet wird am "Großen Rechenbrett"
(Nicht enthalten, aber notwendig:
Rechenwürfel- und Anzahlstangen-Set und Ergänzungs-Set)
Bestellformular
