Individualisierter und kompetenz-orientierter   

Grundlagen- und Förderkurs  

• Prävention  und Aufarbeitung von Rechenstörungen
  
• Verstehendes Erlernen der Grundrechenarten
  
  
     
  Für: Vorschule, 1. und 2. Klasse, schulische Förderarbeit und Dyskalkulie-Therapie
   
                                                                                             Flyer als PDF zum Ausdrucken
                                                                                            

Lückenaufgaben und 10er-Übergänge stellen viele Schüler vor unüberwindbare Probleme

Durch die handelnde Arbeit mit Mengenbildern auf der Rechentafel werden die für die Lösung solcher Aufgaben notwendigen mathematischen Strukturen, wie die Zahlzerlegungen oder der Teil-Teil-Ganzes-Zusammenhang (Tripelstruktur) der Anzahlen sichtbar gemacht.
Die Kinder lernen bei dieser Art der Arbeit, mathematische Problemstellungen handelnd mit Spaß und Freude zu bewältigen, und bauen dabei sichere Vorstellungsbilder von Anzahlen und Rechenhandlungen auf.

Immer wieder werden die Prob­leme von Kindern beim Rechnenlernen in folgender Weise begründet: 

„Mathe, das kann mein Kind nicht. Das liegt bei uns in der Familie!“ 

Wissenschaft und Forschung haben längst bewiesen:        

Rechnenlernen hat nichts mit der Vererbung zu tun.
Jeder Mensch kommt mit einem „angeborenen Zahlensinn“ auf die Welt. 
(Dehaene, Der Zahlensinn)

Darum bietet der Kurs „Freundschaft schließen mit den Zahlen 0 – 10“
viele Spiele, strukturierte Arbeitsmittel und ein bisher einzigartiges Zahlzerlegungsbild-Material.

Er leitet an, den angeborenen Zahlensinn mit Spaß und Entdeckergeist auszuges­talten, und
legt die Grundlagen für mathematisches Denken,
die zur verstehenden Teilnahme am Mathematikunterricht
aller weiteren Schuljahre befähigen.

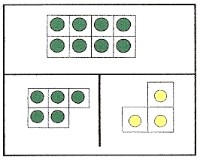
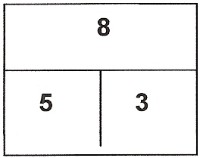
1.) Beginn aller Zerlegungsarbeit ist das konkrete Zusammenbauen und Zerlegen mit Mengenbildern auf der Rechentafel.	2.) Parallel zur handelnden Arbeit auf der Rechen-tafel werden zugleich auch die Zahlzerlegungen mit aufgeschrieben.  Dabei lernen die Schüler von selbst, dass man aus den 3 Zahlen eines  Zahlentripels immer 4 Aufgaben, nämlich 2 Plus- und 2  Minusaufgaben,  bilden kann.
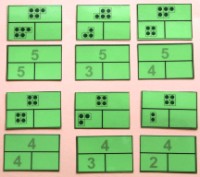
3.) Die von mir entwickelten Anzahlzerlegungsbild-Karten für zwei unterschiedliche Mengenbilder machen die Zahlzerlegungen sichtbar. Die leichter simultan zu erfassenden MBB-Darstellungen im Doppelfünfer-Raster werden bewust schon von Anfang an auch mit den linearen Darstellungen eingeführt, da sie in allen Schulbüchern vorkommen und die Schüler sich so möglichst frühzeitig auch hier über das 10er-Raster oder die 5er-Striche zu orientieren lernen, um das Abzählen von Elementen zu vermeiden.	4.) Zu diesen Anzahlzerlegungsbild-Karten gehören auch zwei verschiedene Sorten von Zahlengleichungen: Eine mit Lücke und eine komplette Plusgleichung zu jeder Zerlegung. Zu diesen Karten habe ich viele verschiedene Spielmöglichkeiten entwickelt.
5.) Zu allen Anzahlkarten habe ich eine Reihe von unterschiedlichen  Lernspielen (Band 4: Spiele) entwickelt, damit die Schüler sich über viele Anwendungsübungen die insgesamt 60 Anzahlbild-Darstellungen sicher einprägen. Hier abgebildet ist das Spiel "Anzahlbilder-Profi-Rennen"	6.) Auf  3 Rechentafeln (10er, 20er, 100er) werden mit den Anzahlege-Materialien Zerlegungen und Aufgaben dargestellt. Auf den Rechentafeln für den 10er und 20er Zahlenraum finden sich verschiedene Raster, die sowohl doppel-reihige Anordnungen, z.B. mit MBB, als auch lineare Anordnungen mit AStB oder Rechenwürfeln ermöglichen.
7.) Als nächstes wird der Fokus auf die Automatisierung des bisher Erarbeiteten gelegt. Über die Wendekärtchen der beiden Varianten des Spiels "Plus wie viel?" werden z.B. zuerst auf der Mengenebene und danach auf der Zahlenebene die zusammengehörigen Zahlentripel automatisiert.	4.) Im 100er-Zahlenraum werden die Rechenaufgaben in gleicher Weise auf der Rechentafel dargestellt; nur werden hier an Stelle der doppelreihigen Mengenbilder nur noch die lineare  Darstellungsform mit den Rechenwürfel als  Arbeitsmittel eingesetzt.
Weiteres Material meines Kurses findet sich unter dem Schalter "Arbeitsmittel"

Durch diesen erfolgreich erprobten Grundlagen- und Förderkurs werden zunächst die mathematisch-logischen Vorläuferfähigkeiten systematisch, zugleich aber auch spielerisch aufgebaut.

Sodann wird ein tragfähiger Zahlbegriff erarbeitet, was schließlich zu einem verstehenden und sicheren Rechnen im 100er-Zahlenraum führt.

         Ziel:   Aufbau der Grundlagen des mathematischen Denkens

Dabei ist alles aufeinander abgestimmt:

• Hintergrundwissen und detaillierte Anleitungen zu allen Übungen im Handbuch
  
• für die Förderung benötigte Arbeitsmittel, Arbeitsblätter und Demo-Karten
  
• viele Spiele, strukturierte Arbeitsmittel und einzigartige Zahlzerlegungsbild-Karten

Gründe für die Entwicklung dieses Grundlagen- und Förderkurses

In all den Jahren meiner Praxis in Schule und Lerntherapie stellte ich immer wieder Folgendes fest:

1.   Bei allen Schüler waren die Rechenstörungen schon zu einem sehr frühen Zeitpunkt des Rechenlernprozesses entstanden und Defizite schon aus dem Mathematikunterricht der 1. Klasse zu finden.

2.   Bei vielen Schülern fanden sich zusätzlich, sogar bis ins Erwach-senenalter hinein, noch Defizite in den eigentlich im Vorschulalter aufzubauenden mathematischen Vorläuferfähigkeiten (wie z.B. der Raum-Lage-Orientierung).

Die Kinder, bei denen ich eine fehleranalytische Förderdiagnose durch-führte, wurden zunehmend jünger und zeigten, obwohl alle einen Kindergarten oder eine Vorschulklasse besucht hatten, bereits in der 1. Klasse deutliche Rechenstörungen, die schon am Schulanfang Ängste, Schulunlust und psychosomatische Störungen nach sich gezogen hatten.

Immer öfter wurden mir auch Schüler vorgestellt, die schon lange schulische und außerschulische Förderzeiten in schulischen Förder-kursen, einer integrativen Förderklasse, bei REBUS, einem sonderpäda-gogischen Förderzentrum oder auch in einer lerntherapeutischen Einrichtung hinter sich gebracht hatten, ohne dabei den Zehnerübergang begriffen zu haben.

Bei der Förderung dieser Schüler, die solche hartnäckigen Probleme aufwiesen, war sehr häufig das Fördermaterial  "Kieler Zahlenbilder" von Christel Rosenkranz eingesetzt worden.
Dieses Material, das damit beworben wird, dass es ein Förderprogramm zum Aufbau des Zahlbegriffs sei, hat jedoch ein großes fachliches Manko:

Es arbeitet mit Zahlenbildern, die unser 
                           dekadisches Zahlensystem (Zehnersystem) 
                           nicht strukturgerecht wiederspiegeln.

Die Zahlbildhäuser - Das Hauptarbeitsmaterial der Kieler Zahlenbilder

Die Kieler-Zahlbild-Häuschen (9 Plätze in je 3 Reihen und ein Platz oben im Dach) verdeutlichen den Schülern die Strukturen der "Kraft der 10" und "Kraft der 5"  nicht einmal im Ansatz.
Die Kieler Zahlenbilder haben keine mathematisch fachwissenschaftlich korrekte Struktur.
Die Schüler lernen hierbei, sich Mengenanordnungen als Zahlbilder einzuprägen, die nichts mit den linearen
10er- oder Doppel-5er-Anordnungen in ihren Schulbüchern gemeinsam haben.
Eine weitere Schwierigkeit ergibt sich daraus, dass jedes Zahlbild eine andere Farbe hat, was der Schüler ebenfalls in keinem Schulbuch wiederfindet und wovon er zusätzlich sich mühsam später wieder lösen muss.
Der Ansatz, viele Übungen anzubieten, über die sich die Schüler feste Anzahlbilder einprägen, ist im Prinzip gut, allerdings sollten solche Zahlbilder immer so strukturiert sein, dass man mit ihnen die Zehnerübergänge darstellen kann und die Schüler daran die dekadische Struktur unseres Zahlensystems in den weiteren Zahlenräumen wiedererkennen können.

Ein so beschaffenes Fördermaterial, das ganz klar mathematisch korrekt stukturiert ist, findet sich u.a. im BASISKURS Mathematik und im MATINKO Lernprogramm von Peter Jansen. Für beide Kurse benutzt Peter Jansen als Arbeitsmittel die einfarbigen Rechenblöcke (1er-Würfel, 10er-Stange, 100er-Platte, 1.000er-Würfel) aus Holz.

Peter Jansen bietet mit beiden Kursen die Möglichkeit, bei den Kindern einen sehr tragfähigen Zahlbegriff, der den ordinalen, den kardinalen und auch den relationalen Zahlaspekt beinhaltet, klar strukturiert nach seinem "Drei-Säulen-Modell" aufzubauen.

Die Erfahrung, dass in der heutigen Zeit im Zeitfenster vom Vorschulalter bis einschließlich der 1. Hälfte des 1. Schuljahr etwas falsch zu laufen scheint, führte mich 2007 zu der Idee, ein eigenes Unterrichts- und Förderwerk zu verfassen. Nach einer längeren Erprobungszeit war es 2009 endlich zur Veröffentlichung fertig.

Mein Grundlagen- und Förderkurs fußt auf dem Jansen'schen "Drei-Säulen-Modell" der Zahlbegriffsentwicklung und erarbeitet mit den Schülern detailliert alle 3 Zahlaspekte. Bei der Entwicklung des Kurses "Freundschaft schließen mit den Zahlen 0 - 10", der ein individualisiertes und kompetenzorientiertes Lernen ermöglicht, lag mir auf Grund meiner vielfältigen Erfahrungen in der lerntherapeutischen Praxis mit Schülern, die schon in sehr jungen Jahren eine starke Abwehrhaltung gegenüber "schwarzen Zahlen" bis hin zu massiven Ängsten gegenüber dem Mathe-matikunterricht aufgebaut hatten, zusätzlich Folgendes besonders am Herzen:

Was mir bei der Entwicklung des Grundlagen- und Förderkurses wichtig war

• Gestaltung von Anzahlbild-Materialien, mit denen sich vielfältige handlungsorientierte Übungen durchführen lassen;
   
• Schaffung fester Mengenbilder-Bausteine (MBB), mit denen die Kinder sich die für sie so schwer zu begreifenden Zahlzerlegungen über konkretes Zerlegen und Zusammensetzen wirklich "erbauen" können;
   
• Erzeugung von Freude an der Beschäftigung mit Zahlen, vor allem bei Schülern, die durch viel Misserfolg bereits sehr desmotiviert sind und richtige Ängste vor Mathematik aufgebaut haben.
  Erreichen wollte ich dieses, indem ihr Spieltrieb intensiv angesprochen wird.
  Daher entwickelte ich spezielle Anzahlbild-Karten und bisher einzigartige Anzahlzerlegungsbild-Karten, mit denen über diverse, aber immer wieder wiederkehrende Spiele als spielerische Übungen sowohl ein tragfähiger Anzahlzahlbegriff als auch die Zerlegungen aller Zahlen bis 10 sicher aufgebaut werden können;
   
• Entwicklung von Arbeitsmitteln, mit denen die Schüler die ebenfalls so langwierig auswendig zu lernenden Aufgaben des kleinen Einspluseins und Einsminuseins spielerisch automatisieren können;
  
• Hinzunahme eines PC-Programms,
  -   das mit den gleichen Mengenbildern arbeitet, nicht viel unnötige Ablenkung bietet, die einzelnen Übungen schnell zugänglich macht und das außerdem über eine auf einfache Weise abrufbare und ausdruck-bare Protokollfunktion verfügt, damit man den Schülern zeigen kann, ihren Lernfortschritt bei kontinuierlicher Arbeit selbst zu verfolgen,
  -   das zugleich aber auch ein Programm ist, das den Lehrenden und Eltern einen schnellen Überblick über den Lernstand und die Lernentwicklung des Kindes gibt.
  
• An-die-Hand-Gabe von Hilfen für Lehrer und Eltern, um bei sich und den Kindern einen klaren "mathematischen Wortschatz" aufbauen zu können.

Näheres zu möglichen Vortrags- und Fortbildungsthemen zur Vorstellung und Einweisung in dieses Grundlagen- und Förderwerk siehe unter Schalter "Fortbildungen".

Individuelle Wünsche können Sie gerne persönlich mit mir abstimmen.
Nehmen Sie dafür bitte über das Kontaktformular oder per  E-Mail Kontakt mit mir auf; nennen Sie mir bitte Ihre Telefonnummer und wann ich Sie am besten erreichen kann.
Ich werde mich sobald wie möglich bei Ihnen telefonisch zurückmelden.