
| | 
| | 
|
| Abb. 1 | | Abb. 2 | | Abb. 3 |
Abgebildet sind hier 30 der von mir entwickelten insgesamt
60 Anzahlbild-Karten als grundlegen-
des Arbeitsmittel.
Der Kurs arbeitet von Anfang an mit
6 verschiedenen Anzahldarstellungen,
wobei die Schüler lernen sollen, Vorstellungsbilder von ihnen aufzubauen:
1. Mengen-Bilder-Bausteine
2. Finger-Bilder
3. Strich-Bilder
4. Würfel-Bilder
5. Steckwürfel-Bilder im 10er-Raster
6. Rechenwürfel-Bilder | | Anzahlfolgen gelegt mit
Anzahl Stangen-Bausteine (AStB), Mengen-Bilder-Bausteinen (MBB) und Rechenwürfeln
(immer von links nach rechts)
Auf der Darstellung ist auf einen Blick deutlich zu erkennen, dass die rechten und linken Anzahldarstellungen beide die 5er-Struktur besitzen.
So kann z. B. die 8 als aus den 2 Teilportionen (5 + 3) schnell bestimmt werden, ohne dass man abzählen muss. | | Im Zahlenraum 11 - 20 sieht man,
dass den drei Anzahldarstellungen
gemeinsam ist, dass sie alle mit der
"Kraft der 10" arbeiten.
Der "10er" wird als eine besondere feste Einheit dargestellt.
Sowie 10 Elemente zusammen-gekommen sind, wachsen sie zum speziell gekennzeichneten "festen"
10er-Verbund zusammen.
So wird den Kindern das Überschrei-
ten eines Zehnerüberganges ganz bewusst. |
| | | | | |
 | |  | | 
|
| Abb. 4 | | Abb. 5 | | Abb. 6 |
Band 2 des Kurses "Freundschaft
schließen mit den Zahlen 0 - 10"
beinhaltet viele Arbeitsmittel für die unterschiedlichsten Übungen zur
handelnden Erarbeitung eines trag-
fähigen Zahlbegriffs:
die Anzahlbild-Karten, MBB und AStB, Rechentafeln, ... | | Hier ist eine Anzahlfolge mit Anzahlbild-Karten, Wendeplättchen und Karten mit den Zahlnamen gelegt, bei deren Aufbau der Schüler die wichtige Entdeckung macht, dass "von einer Zahl zur nächsten immer genau ein Element mehr dazu kommt". | | In Band 4 des Kurses ist eine umfangreiche Spielesammlung zur Automatisierung von Anzahlbildern,
den Zahlzerlegungen sowie der Auf-gaben des kleinen Einspluseins und Einsminuseins zu finden. |
| | | | | |

| |  | |  |
| Abb. 7 | | Abb. 8 | | Abb. 9 |
Die 60 Anzahlbilder der 6 verschie-
denen Anzahldarstellungen im
Zahlenraum bis 20 werden durch viele verschiedene Spiele mit den
Anzahlbild-Karten automatisiert, und
der Schüler baut feste Vorstellungsbilder von ihnen auf.
Beim "Anzahlbilder-Memory" gilt es,
wie allgemein beim Memory Spielen, zwei zusammen passende Karten auf-zudecken, die man sodann als Pärchen an sich nehmen darf.
Zwei Karten passen zusammen, wenn auf ihnen eine gleiche Menge von Elementen dargestellt ist.
Die Spieler bestimmen mit dem "Blitz-blick", wie viele Elemente jeweils auf
den aufgedeckten Karten zu sehen
sind und ob es gleich viele sind.
Oben ist gerade ein MBB-5er und ein Strichbild-5er aufgedeckt worden, die
ein 5er-Pärchen bilden. | | Beim Spiel "Wie viele? - Gleich viele!" haben hier 4 Spieler je eine Karte vom Stapel Ihrer Anzahlbild-Karten aufge-deckt. Auf das Kommando "Wie viele?" gilt es, mit dem Blitzblick schnell die jeweils auf den Kärtchen darge-stellten Anzahlen zu bestimmen und zu vergleichen.
Hat ein Spieler Kärtchen entdeckt, auf denen gleich viele Elemente dargestellt sind, so ruft er "Gleich viele!"
Nun muss er allerdings die Karten auch benennen können.
Sagt er im dargestellten Fall:
"Ein Würfelbild-3er, ein Fingerbild-3er und ein Rechenwürfel-3er haben gleich viele Elemente", darf er diese drei Karten an sich nehmen. | | Beim Spiel "Anzahlbilder-Profi- Rennen" wird mit 5 Sorten von Anzahlbild-Kärtchen gespielt.
Es liegen 50 Karten auf dem Spielplan. Jeder Mitspieler hat einen Sammelplan, mit 10 Feldern, und es gilt nun, je eine Anzahlbild-Karte der Mengen 1 - 10 darauf zu sammeln. Jeder Mitspieler
hat eine Spielfigur und einen Würfel. Er wandert die jeweils erwürfelte Anzahl von Schritten auf dem Spielplan vorwärts. Der Spieler nimmt sich die zu der Farbe des jeweiligen Feldes gehörige Sorte von Anzahlbild-Karten, auf dem die Spielfigur zum Stehen kommt, und sucht sich die Menge heraus, die zu der Zahl auf dem Spielfeld passt. Wer zuerst seinen Sammelplan voll besetzen kann, gewinnt. |
| | | | | |
 | | 
| |  |
| Abb. 10 | | Abb. 11 | | Abb. 12 |
Beim Spiel "Im großen Zahlenwald"
geht es darum, sich die Mengenbilder der Anzahlen 6 - 10 der vier verschie-denen Anzahlbild-Darstellungen ein-zuprägen.
Es gilt nun, das jeweilige MBB- oder AStB-Bild, auf dem man gerade auf dem Spielplan zu stehen kommt, auf dem Sammelplan mit Wendeplättchen und Hölzchen als Würfel- und Strichbild darzustellen. | | Im Mengenbilder-Baukasten lassen sich die MBB-Kärtchen gut sortieren und schnell auffinden.
Mit den Mengen-Bilder-Bausteinen können die Kinder in vielen spielerischen Übungen, wie z. B. beim MBB-Angeln, beim MBB-Würfeln, beim Einrichten der Zahlenwohnungen und beim Zerlegen und Zusammensetzen von Mengen auf der Rechentafel handelnd Anzahlen begreifen und einen tragfähigen Zahlbegriff aufbauen. | | Zur systematischen Erarbeitung aller Zerlegungen einer Zahl versucht der Schüler zunächst, alle Möglichkeiten zu finden, wie er die jeweilige Anzahl aus zwei MBB zusammensetzen kann.
Um die in den Schulbüchern gebräuchliche Form der linearen Darstellung aufzunehmen, kann
sodann mit rot-blauen AStB oder auch mit Steckwürfel-Stangen gebaut werden. Auch mit Kugelketten von festen Anzahlen, die am Anfang und Ende fest verknotet sind, sodass die Kugeln nur hin und her geschoben werden können, lassen sich Zahlzer-legungen gut darstellen. |
| | | | | |

| |  | |  |
| Abb. 13 | | Abb. 14 | | Abb. 15 |
Mit dem Anzahlegematerial der Mengen-Bilder-Bausteine (MBB), der Anzahl-Stangen-Bausteine (AStB) und der Rechenwürfel mit 5er-Markierungen haben die Schüler ein strukturiertes Anschauungs- und Arbeitsmaterial zur Verfügung, das unser Zehner-Zahlensystem gut veranschaulicht. Es eignet sich sowohl zum Erarbeiten der Zahlzerlegungen als auch zum Lösen von Plus- und Minusaufgaben mit Stellenwertübergängen auf der Rechentafel.
Außerdem verfügen alle drei Materialien auch über eine besondere Einheit/ Kennzeichnung des "vollen Zehners" (10er-Rechenwürfel = feste 10er-Stange, 10er-MBB = 10er mit einem roten Spanngurt, 10er AStB = 10er mit einem roten Spanngurt. | | Für drei Zahlenbereiche habe ich Rechentafeln erstellt.
Bei der Erarbeitung der Zahlzerlegungen wird auf der 10er-Rechentafel gearbei-tet, bei den ersten Aufgaben mit Zehner-überschreitungen auf der 20er-Rechen-tafel. Bereits nach der systenatischen Erarbeitung aller Zahlzerlegungen erweitere ich den Zahlenraum bis 100, damit den Kindern so das Prinzip der Stellenübergänge als ein allgemein-gültiges und nicht nur als ein auf den 20-Zahlenraum beschränktes bewusst wird. Dazu wird dann parallel 20er-Tafel auch schon die 100er-Rechentafel ein-geführt. | | Nach der handelnden Arbeit mit den MBB im Zuge der systematischen Erarbeitung aller Zahlzerlegungen wird immer auch das Handeln in der Vorstellung geübt. Die Schüler
zeichnen dazu z.B. die Zerlegungen mit selbst-gestalteten MBB auf.
Zur Vertiefung stehen diverse Arbeitsblätter zur Verfügung (Band 3), die zunächst noch mit der MBB-Darstellung arbeiten.
Mit dem obigen AB kann z.B. der Automatisierungsgrad der Zahlen-partner noch auf der gemischten Mengen- und Zahlebene überprüft werden.
Die letzte Stufe stellen AB dar, auf
denen sich nur noch Rechentafeln mit Zahlen ganz ohne Mengenbilder befinden. |
| | | | | |

| |  | |  |
| Abb. 16 | | Abb. 17 | | Abb. 18 |
Sodann geht es um die sichere Auto-matisierung der Zerlegungen aller Zahlen bis 10.
Dazu stehen im Band 4 diverse Übungs-spiele zur Verfügung.
Aus 5 Bögen dieser roten Mengenbild-Kärtchen wird das Spiel "Zu wenig! - Zu viel! - Genau X!" hergstellt.
Die Spielkarten werden, je nachdem welche Zahlzerlegung gerade trainiert werden soll, entsprechend aussortiert. | | Die Abbildung zeigt das Spiel "Zu wenig! - Zu viel! - Genau 5!".
Für dieses Spiel werden nur alle 0er - 5er-Karten benötigt. Die anderen 6er- 10er-Karten werden bei Seite gelegt. Jeder Spieler bekommt die Hälfte der Karten und legt sie als verdeckten Stapel vor sich hin. Auf ein Kommando hin drehen beide Spieler gleichzeit ihre oberste Stapelkarte um und vergleichen blitzschnell, ob die beiden Mengenbilder zusammen einen 5er ergeben.
Zu Anfang können am Spielrand noch die möglichen MB-Kombinationen der jeweiligen Zahl ausgelegt werden. Mit zunehmender Speicherung der 5er-Partner kann dies unterbleiben. | | Eine weitere Übungsmöglichkeit für
die Automatisierung der Zahlzerlegungen stellen neben den konkreten Handlungen mit Lege-material auf der Rechentafel, den Arbeitsblättern und Spielen auch die Budenberg Lernprogramme mit den bekannten MBB-Darstellungen für den PC dar. |
| | | | | |
| | 
| |  |
| Abb.19 | | Abb. 20 | | Abb. 21 |
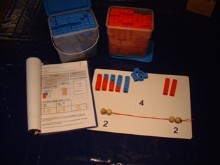
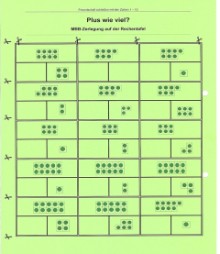
Eine weitere Übungsmöglichkeit für alle Zahlzerlegungen bietet das Spiel "Plus wie viel?".
Den Wendekarten entnehmen die Schüler, um welche Menge es jeweils geht.
Auf der Rechentafel erkennen sie im unteren Bereich jedoch nur eine Teil-menge. Sie sollen nun herausfinden, welches die zweite Teilmenge ist. | | Der Schüler sieht sich die Wendekarte in der Mitte oben an und fragt:
" Ein 3er plus wie viel ist ein 5er?"
Auf der Rückseite kann er kontrollieren, ob sein Ergebnis richtig ist.
Dieses Spiel liegt in zwei Versionen vor:
Bei der ersten Version sind beidseitig Mengenbilder zu sehen,
bei der zweiten nur noch Zahlen. | | Einige Arbeitsblätter können die
Schüler konkret mit ihren MBB aus-
legen und anschließend deren Um-risse einzeichnen.
Bei der hier dargestellten Einführung
der Gleichungen lernen sie im Übrigen gleich beide Gleichungsformen kennen:
Bei der einen steht die Summe ("die größte Zahl des Zahlentripels") rechts vom Gleichheitszeichen, bei der anderen links. |
| | | | | |

| |  | |  |
| Abb. 22 | | Abb. 23 | | Abb. 24 |
| Einen besonderen Stellenwert für die systematische Erarbeitung aller Zahlzerlegungen stellt das von mir entwickelte und bisher einzigartige Anschauungsmaterial der Anzahl-zerlegungsbild-Karten dar. | | Zuerst wird geübt, die beiden unter-schiedlichen Bildkartentypen einander zuzuordnen. Dabei entdecken die Schüler schnell die Umkehr- und Tauschaufgaben und sind schnell in der Lage, Begründungen dafür anzugeben.
Bei der nächsthöheren Schwierigkeitsstufe kommen dann Zahlzerlegungs-Karten hinzu. | | Zahlzerlegungskarten gibt es in 2 Versionen:
Einmal die MBB-Zerlegungs-Karten
und dann die der linear angeordneten Steckwürfelstangen. Beide Formen haben ein unterlegtes 10er-Raster.
Die Schüler können sich bei der Mengenschnellerkennung an den jeweils freien Plätzen oder an dem
5er-Strich orientieren. |
| | | | | |
 | |  | | 
|
| Abb. 25 | | Abb. 26 | | Abb. 27 |
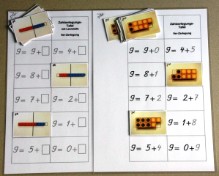
Die Anzahlzerlegungsbild-Karten lassen sich zwei unterschiedlichen Gleichungs-typen zuordnen:
den Gleichungen mit Leerstelle und
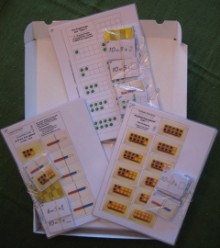
den kompletten Gleichungen. | | Als besondere Variante des Kartenein-satzes lassen sich, wenn das Kind sich weitgehend sicher bei den Zerlegungen der jeweiligen Zahl ist, auch verschiede-ne Bingo-Spiele durchführen, bei denen die Zerlegungen beim Schüler nach mehrmaligem Einsatz schnell gesichert sind. | | Diese Zahlzerlegungsbild-Materialien habe ich für alle Zahlen von 2 - 10 erstellt. Zu jeder Zahlzerlegung gehören 6 Spielpläne und 4 Kartensätze. |
| | | | | |
 | |  | | 
|
| Abb. 28 | | Abb. 29 | | Abb. 30 |
Folgendes Material dient ebenfalls der Automatiesierung:
Für alle 2 x 144 Aufgaben des kleinen Einspluseins habe ich Aufgabenklärt-chen hergestellt, farblich verschieden jeweils für die Zahlenräume bis 5, bis 8, bis 10 und bis 20. | | Mit den Bingo-Kärtchen lassen sich 2 Spielvarianten spielen:
"Bingo"
"Langer und kurzer Zahlname"
Die obige Darstellung zeigt eines der insgesamt 5 verschiedenen Bingo-Spiele.
Auf Abb. 28 wird mit den gleichen Karten das Spiel "Langer und kurzer Zahlname" gespielt.
Die Ziffernkarten gelten dabei als "kurze Zahlnamen" und die Plus- und Mimus-aufgaben als "langer Zahlname" | | Die Aufgabe 6 + 7 wurde auf den Rechentafeln mit den beiden Anzahlmaterialien (grüne und gelbe
MBB und rote und blaue AStB) gelegt.
Nachdem der Schüler den 1. Sum-manden (erste Teilmenge) in den
linken Bereich der 20er-Tafel gelegt hat, erkennt er, dass in das 10er-Feld noch ein 4er hinein passt. Daraufhin
tauscht er den 2. Sumanden, den 7er,
in zwei andere MBB um, von denen
einer (der 4er) für die 10er-Ergänzung verwendet wird.
Übrig bleibt der 3er, der im nächsten 10er-Feld landet. |
| | | | | |
 | |  | |  |
| Abb. 31 | | Abb. 32 | | Abb. 33 |
Mit dem Material der
"Kressel'schen 100er-Kästen"
wurden hier Aufgaben mit 10er-Über-gang durch eine zweifarbige Gestaltung in Ihrer Struktur deutlich gemacht.
Außerdem wurde parallel mit zwei verschiedenen Mengenanordnungen
gearbeitet.
Ich lasse Schüler zuerst mit den Doppelfünfer-Kästen arbeiten und sie die Würfel der beiden Summanden-mengen in MBB-Form anordnen.
Der Schüler erkennt im 10er-Kasten auf einen Blick, dass noch ein 2er hinein passt, bis der 10er voll ist. Wenn er die 5er-Würfelmenge des 2. Summanden nun in zwei Teilmengen aufteilt, von denen ein Teil die 10er Ergänzung also eine 2er-Menge ist, so sieht er, dass die zweite Teilmenge des 5ers ein 3er ist. Den 2er legt er zur Ergänzung
des 10ers in den linken Kasten mit den roten Würfeln des 1. Summanden. Den Rest vom 2. Summenden legt er in den nächsten Kasten.
Deutlich ist zu erkennen, dass aus 8 + 5 Würfeln nun ein voller 10er und ein 3er geworden ist, es zusammen also 13 Würfel sind.
Wichtig ist mir bei aller handelnden Erarbeitung von Rechenaufgaben mit Anschauungsmaterial, dass stets parallel zum Legen von Aufgaben auch das Aufschreiben von Zahlen, das Legen von Zahlenkärtchen sowie das Beschreiben der Handlungen geübt wird.
Die zweifarbige Stellenwertdarstellung der Summe im obigen Beispiel dient dabei der visuelle guten Unterscheid-barkeit von Zehnern und Einern. | | Die "Kressel'schen 100er-Kästen" bestehen aus zwei Grundkästen mit jeweils zehn Doppelfünfer-Kästen und zehn 10er-Kästen in linearer Anordnung. Dazu gehören 101 Holzwürfel, deren 4 Seiten unter-schiedlich gestaltet sind.
Zur Kenntlichmachung zweier Mengen gibt es je eine rote und eine grüne Seite. Die anderen beiden Seiten weisen die Zahlnamen von 0 - 100 auf, wobei die Ziffern auf der einen Seite einfarbig schwarz sind und auf der anderen Seite Zehner und Einer zweifarbig rot / grün kenntlich machen.
Mit diesen beiden unterschiedlichen Kästen lasse ich die Schüler Anzahlen im 100er Zahlenraum immer auch schon in der für sie schneller simultan
zu erfassenden doppelreihigen MBB-Anordnung und zugleich parallel dazu
in der in allen Schulbüchern gebräuch-lichen linearen Anordnung darstellen.
Ich habe die Erfahrung gemacht, dass die Schüler mit der linearen Anordnung recht bald keine Probleme mehr haben, wenn die Orientierung in beiden Darstellungen von Anfang an parallel eingeübt wird.
Eine Parallele dazu findet sich auch schon bei der Erarbeitung des 10er- und 20er-Zahlenraums, indem dort auf den 10er- und 20er-Rechentafeln Strukturraster für die Arbeit mit MBB und AStB vorhanden sind. | | In den Doppelfünfer-Kästen
orientieren sich die Schüler zur Mengen-Schnellerfassung bei Mengen ab 5 Elementen an den gut erkenn-baren freien Plätzen in den 10er-Kästen und bestimmen die Mengen so über die besonders gut automatisierten
10er-Ergänzungen (10er-Partner).
Beispiel oben rechts:
"Da sind noch 4 Plätze frei, dann liegen schon 6 Würfel im Kasten!"
Bei den 10er-Kästen in linearer Anordnung wird neben der 10er-Ergänzung auch die Orientierung an
der 5er-Markierung speziell trainiert.
Beispiel oben links:
" Alle Plätze bis zum 5er-Strich sind besetzt und einer danach. Ein 5er und ein 1er zusammen ergeben einen 6er."
Die Orientierung an 10er- und 5er-Markierungen im Sinne der "Kraft der 10" und "Kraft der 5" spielen bei der Mengenerfassung eine wesentliche Rolle.
Wichtig darüber hinaus ist mir bei aller Arbeit mit strukturiertem Material, dass die Schüler gleichzeitig angeleitet werden, einen mathematische Grundwortschatz aufzubauen, mit
dem sie ihr mathematisches Handeln zu beschreiben lernen.
Die Orientierung an 10er- und 5er-Markierungen im Sinne der "Kraft der
10" und "Kraft der 5" spielen bei der Mengenerfassung eine wesentliche Rolle. |
| | | | | |

| |  | | 
|
| Abb. 34 | | Abb. 35 | | Abb. 36 |
Die Struktur unseres Zehner-Zahlensystems spiegeln die Rechenwürfel mit ihren 1er-Würfeln, den 10er-Stangen und den
100er-Platten gut wieder und zeigen deutlich, dass die folgenden Zahlen-räume die gleiche Struktur aufweisen:
10 x 1er-Würfel = 10er-Stange
10 x 10er-Stange = 100er-Platte
10 x 100er-Platte = 1.000er-Würfel
Diese dekadische Struktur setzt sich in allen folgenden Zahlenräumen fort:
So kann man das Folgende zwar mit
den Schülern nicht mehr mit konkreten Würfeln legen, allerdings lassen sich 10.000, 100.000 und 1.000.000 Würfel-mengen gut zeichnerisch als Stangen, Platten und wiederum als Würfel in folgender Weise darstellen:
10 x 1.000er-Würfel = 10.000erStange
10 x 10.000er-Stange = 100.000er-Platte
10 x 100.000er-Platte = 1.000.000er-Würfel
Mit dem Hineinlegen von Rechen-
würfeln ins Zahlenhaus erarbeite ich
mit den Schülern das Stellenwert-system.
Mit der Hausnutzungsordnung, dass sich immer nur 9 Elemente einer Sorte zugleich in einer Wohnung aufhalten dürfen, werden auch die Stellenwert-überschreitungen sichtbar gemacht.
Sollen zu den obigen 1.356 Würfeln
267 Würfel dazu kommen, so legt der Schüler die entsprechende Anzahl an Würfelmengensorten in die jeweilige Wohnung dazu. Gemäß der Wohnungs-ordnung bündelt er anschließend in jeder Wohnung jeweils 10 Elemente, tauscht sie in die nächste Einheit um
und lässt sie in die nächst höhere Wohnung wechseln. | | Auf der Rechentafel ist die Tripelstruktur der Plus- und Minusaufgaben gut zu erkennen.
Bei der Erarbeitung der Zahlzerlegungen auf der Rechentafel haben die Schüler die Teil-Teil-Ganzes-Struktur der Zahlen als gegliederte Quantitäten erkannt und wissen daher, dass ein Ganzes (im großen Kasten oben auf der Rechen-tafel) aus zwei Teilen (die beiden klei-neren Felder unten auf der Rechentafel) zusammengesetzt werden kann.
Parallel zum Zusammenschieben, "Bauen" mit MBB, AStB, Rechenwürfeln o.ä. stellen die Schüler dazu Plusauf-gaben auf.
Zur Handlung des Wegnehmens oder Herunterschiebens schreiben sie Minusaufgaben. Dabei schieben sie einen Teil vom oberen Ganzen weg in eines der unteren Teilmengenfelder und stellen daraufhin fest, dass dies der oben nun übrig bleibende Rest die zweite Teilmenge ist.
Durch wiederholtes Zusammenschieben und Zerlegen wird den Kindern auch die Bedeutung der Umkehraufgaben
von selbst bewusst. Ebenso erkennen sie die Bedeutung der Tauschaufgaben. Wichtig für die Mengenschneller-fassung ist es, neben den besonders hervorgehobenen 5er- und 50er- Markierungen auf den Rechentafeln auch die 10er-Stangen, die 100er-Platten und den 1.000er-Würfel der Rechenwürfel zu markieren.
Unmarkierte Rechenwürfel verleiten die Schüler sonst nur wieder zum Abzählen. | | Das Herunterschieben einer Teil-menge vom Ganzen in ein Teilmen-genfeld nutzen die Schüler z. B. auch
zur Bestimmung des Unterschieds zwischen 2 Zahlen.
Bei der obigen Darstellung geht es um die Aufgabe, den Unterschied
zwischen 65 und 17 zu bestimmen.
Dafür hat der Schüler 65 Rechenwürfel in das obere Feld fürs Ganze gelegt
und sodann 17 Rechenwürfel in ein
Teilmengenfeld geschoben. Nun kann er schon sehen, dass die verbleiben-den 48 Rechenwürfel die zweite Teilmenge und damit den Unterschied bilden. Damit hat er auch schon das Rechenverfahren erkannt, das zur Unterschiedsbestimmung nötig ist.
Er stellt parallel zur Handlung
folgende Rechenaufgabe auf:
65 - 17 = 48
Hat der Schüler die Teil-Teil-Ganzes-Struktur verstanden, so kann er mit einem Zahlentripel insgesamt 12 Plus- und 12 Minusaufgaben lösen oder selbst aufstellen.
(Siehe dazu: "Frühförderung", Aufgabenbereiche A - F. Unter Punkt E sind alle 24 möglichen Aufgaben zu einem Tripel aufgeführt.) |
| | | | | |