Kompetenzstufen
beim Aufbau mathematischer Verständnisgrundlagen
Einen genauen Überblick über die Kompetenzen beim Aufbau mathematischer Verständnisgrundlagen, die Ihr Kind schon
zu Schulbeginn entwickelt haben sollte, und über diejenigen Kompetenzen, die im Laufe des 1. Schuljahres entwickelt
werden müssen, um dann im 2. Schuljahr die Multiplikation verstehen zu können, finden Sie in den folgenden Kompetenzrastern, mit Hilfe derer Sie als Lehrer und Therapeuten, aber auch als Eltern und Erzieher einen Überblick bekommen über die klare Aufstellung aller genauestens aufeinander aufbauenden Kompetenzstufen, von den Vorläuferfähigkeiten bis zur Multiplikation.
Diese Kompetenzstufen zu kennen ist deshalb so entscheidend wichtig, weil in der Mathematik alle Erkenntnisstufen aufeinander aufbauen und es zu Störungen im Prozess des Rechnenlernens kommt, wenn auch nur die kleinste Stufe ausgelassen wird.
Diese Kompetenzstufen beim Aufbau mathematischer Verständnisgrundlagen zu kennen ist für Lehrer, Therapeuten, Erzieher und Eltern notwendig, um
Defizite erkennen zu können,
das Kind genau dort abholen zu können, wo es steht,
das Kind ganz individuell differenziert fördern zu können,
Rechenstörungen präventiv verhindern zu können.
Um Rechenstörungen zu verhindern, finden Sie unter dem Schalter "Vorläuferfähigkeiten" die vor Schulbeginn zu erlangenden Kompetenzen aufgelistet.
Unter dem Schalter "Frühförderung" finden Sie detailliert aufgelistet, was es im Vorschulalter zu üben gilt:.
Unter "Fotos vom Kurs" können Sie sich anschauen, wie ich solche Übungen in meinen Frühförderkursen mit Vorschülern und Erstklässlern praktisch umgesetzt habe.
Wichtig ist für alle Lehrer, Therapeuten, Erzieher und Eltern zu wissen, dass sich alle Verständnisdefizite in den mathematischen Grundlagen nicht eines Tages von selbst auflösen!
Daher ist es notwendig, immer so schnell wie möglich zu reagieren, wenn
- ein Schüler zählend zu rechnen beginnt,
- für die Lösung von Rechenaufgaben sehr lange Zeit braucht oder
- Mathematik als Fach ablehnt.
Ein Schüler mit Defiziten braucht in jedem Fall Anleitung, um seine defizitäre Erkenntnisschritte nachvollziehen zu können.
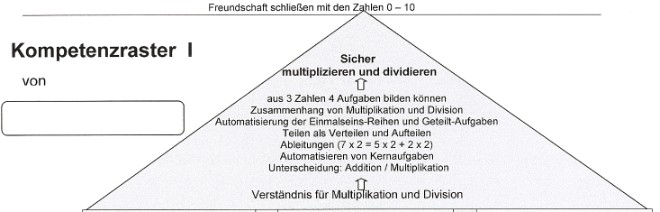
Im Mathematikunterricht muss auf jeden Fall die Aufeinanderfolge der im folgenden Kompetenzraster I ausführlich aufgeführten feinen Verständnisstufen berücksichtigt werden, da das Fehlen auch nur einer Kleinigkeit stets das Verständnis der darüberliegenden Stufen beeinträchtigt.
Achtung: Das folgende Kompetenzraster einschließlich Kellergeschoss von unten nach oben lesen!
Das nachfolgende "Kompetenzraster I" in Anlehnung an das "Drei-Säulen-Modell" von P. Jansen wurde von mir weiter ausdifferenziert.
 |
. |

|
|

|
|
 |
|
 |
|
 |
| |
Die von hier aus bis zum Dachfirst folgenden mathematischen Kompetenzen müssen im Laufe des 1. und Anfang des
2. Schulhalbjahres erworben werden. Ohne sie kann kein Verständnis für die Multiplikation und Division entwickelt
und können die Reihen des kleinen 1x1 nicht sicher gespeichert werden. |
| |
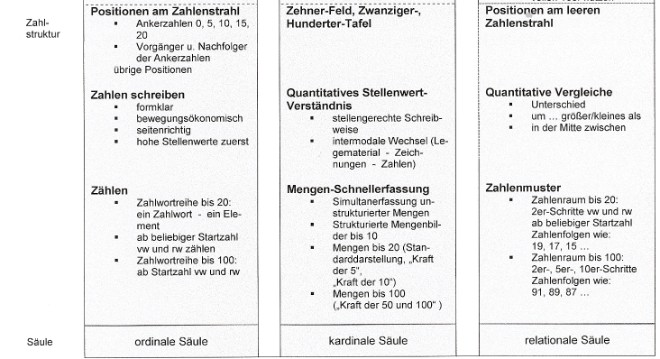
Vom Erdgeschoss an werden die Kompetenzen nach 3 verschiedenen Zahlverwendungsarten getrennt untersucht:
1.) Beim ordinalen Zahlaspekt gibt die Zahl die Position eines Elementes in einer Folge wieder.
Er wird auch als Ordnungszahlaspekt bezeichnet (der 3. In der Reihe).
2.) Beim kardinalen Zahlaspekt beschreibt die Zahl die Mächtigkeit einer Menge (ein 3er beinhaltet 3 Elemente).
3.) Beim relationalen Zahlaspekt beschreibt die Zahl eine Beziehung zwischen zwei Zahlen (der Unterschied
zwischen einem 5er und einem 2er ist ein 3er). |
| |
 |
| |
Die Kompetenzen dieses Kellergeschosses müssen im Vorschulalter bis zur Einschulung aufgebaut werden, da
ohne sie das Kind nicht verstehend am Mathematikunterricht des 1. Schuljahres teilnehmen kann.
Wie diese Kompetenzen anzuleiten sind und was genau das Kind können soll, wird unter Schalter "Frühförderung"
detaillierter aufgeführt. |
|
Um eine Übersicht über den jeweils aktuellen Lernstand eines Kindes zu erhalten, sollte sukzessive, immer
wenn eine neuerworbene Kompetenz vom Kind nachgewiesen wurde, dieses im Raster mit Markern
farblich unterschiedlich für die verschiedenen Zahlenräume (10er, 20er, 100er) gekennzeichnet werden.
Dadurch ist dann aus diesem Raster stets der aktuelle Lernstand eines Kindes sowie auch die Zone seiner
nächsten Entwicklung zu entnehmen.
Näheres zur unterrichtsimmanenten Lernbeobachtung und individuellen Förderdiagnostik siehe Schalter "Diagnostik" |
| |
Kompetenzraster II (prozessorientierte Kompetenzen)
Prozessorientierte Kompetenzen nach den Bildungsstandards der KMK vom 15.10.2004
1.) Problem lösen
2.) Kommunizieren
3.) Argumentieren
4.) Modellieren
5.) Darstellen
Kompetenzraster III
(Kompetenzen nachhaltigen Mathematik-Unterrichts)
1.) Stufenfolge des Aufbaus mathematischer Einsichten kennen
2.) Lernausgangslage des Kindes und Zone seiner nächsten Entwicklung ermitteln
3.) Kind dort abholen, wo es im Verständnis steht
4.) Kind durch entsprechend vorbereitete Lernumgebung und gezielte Anleitung zu nächstmöglichen Einsicht führen
5.) Bei der Erarbeitung aller Inhaltsbereiche Stufenfolge berücksichtigen
6.) Mathematischen Grundwortschatz mit dem Kind erarbeiten
Anleitung zum „lauten Denken“ = gezielte Sprachvorbilder geben und Kinder anleiten, alles mathematische Handeln, die Erkenntnisse über Sachverhalte und Einsichten in Zusammenhänge, Gemeinsamkeiten und Unterschiede
sprachlich auszudrücken.
- Stets auffordern zum sprachlichen Begründen mathematischer Aussagen und Vermutungen
- Kind anleiten, eigene Lösungen durch sprachlich begleitete Darstellungen zu überprüfen
7.) Ausgewogenen Wechsel planen zwischen größtmöglicher Individualisierung und angeleitetem Unterricht
8.) Kompetenzorientierung: Kompetenzen (grundlegende Einsichten und Fertigkeiten) individuell absichern
9.) Arbeitsergebnisse des Kindes fehleranalytisch auswerten
10.) Fehler als „Lernanlässe“ auffassen und konstruktiven Umgang mit Fehlern vermitteln
11.) Mit dem Kind gemeinsam in regelmäßigen Abständen seine Lernentwicklung reflektieren
12.) Dem Kind zur Selbständigkeit verhelfen ...
beim Lösen von Aufgaben,
- beim eigenständigen Kontrollieren seiner Arbeitsergebnisse.
- Zur angemessenen Selbsteinschätzung der eigenen Fähigkeiten bei aller Individualisierung stets das kooperative Miteinander und die Teamfähigkeit des Kindes fördern.
Auf dem Weg zum Ziel des abstrakten Umgangs
mit Zahlen, Operationen, Mustern und Strukturen
darf kein Kind verloren gehen!