Mathematische Frühförderung

Gut entwickelte Vorläuferfähigkeiten bei Schulanfang sind
der Garant für schulischen Erfolg

 Den frühen mathematischen Kenntnissen oder Vorläuferfähigkeiten kommt, wie man heute definitiv weiß, eine ganz entscheidende Bedeu­tung für die Ent­wicklung späterer schulischer Leistungsfähigkeit in Mathematik zu.

Von folgenden Fähigkeiten kann, inzwischen empirisch belegt, angenommen wer­den, dass sie vorhanden sein müssen, wenn die Schule erfolgreich absolviert werden soll:           

• Seriation
• Mengenvergleich
• Erkennen von Invarianz
• Operieren mit Eins-zu-Eins-Zuordnungen
• Zahlenwissen (Kenntnis der Zahlbilder bis 10, Zuordnung von Zahlbildern zu akustisch vorgegebenen (genannten) Zahlen im Zahlenraum bis 20) 
• Zählfertigkeiten (vorwärts und rückwärts zählen, Vorgänger und Nachfolger bestimmen)
• Erste Rechenfertigkeiten (im Umgang mit konkretem Material) 

Mit Hilfe dieser vor Schulbeginn überprüften Vorläuferfähigkeiten konnten 60 % der rechenschwachen Kinder bereits im Vorschulalter korrekt identifiziert werden. 
Untersuchungen von K. Krajewski (2003) und Weißhaupt, Peukert und Wirtz (2006) belegen, dass die mathematischen Fähigkeiten gegen Ende des Vorschulalters die späteren Rechenleistungen noch 4 Jahre später entscheidend beeinfluss­ten. 

Kinder mit geringem vorschulischem Wissen bleiben in der Regel „schlechte Rech­ner“, auch wenn sie natürlich durch den Unterricht dazulernen.
Da aber mathematische Kenntnisse systematisch aufeinander aufbauen, ist ein frü­hes Verständnis der Mathematik und mathematischer Vorläuferfähigkeiten für das spätere Lernen unabdingbar. 

So erwerben Kinder mit Schwierigkeiten im Rechnenlernen über Jahre hinweg kaum effektive Rechenstrategien. Ostad stellte bereits 1997 fest, dass schwache Siebt­klässler noch zu 97% Zählstra­tegien beim Rechnen anwandten.

Die beste Frühförderung in der Mathematik besteht darin, diese Wissenschaft als das erfahren zu lassen, was sie ihrem Wesen nach ist, nämlich eine

Wissenschaft von Mustern, Regeln und Gesetzmäßigkeiten.

Der Kurs „Freundschaft schließen mit den Zahlen 0 - 10“ bietet neben vielem Anderen auch Zahlenmuster (Anzahl­bilder) und geometrische Muster zur aktiven Erforschung.
Konkrete Muster und Strukturen bilden die unerlässliche Grundlage für abstrak­te mathematische Strukturen, mit denen die Kinder sich von der 1. Klasse bis zur Berufsbildung immer wieder beschäftigen müssen.
Zahlen und Formen sind keineswegs nur eine Sache des Kopfes, sondern hängen eng mit motorischen Erfahrungen und Emotionen zusammen.
Die Frühförderung im Vorschulalter, ob in einer Kindertageseinrichtung oder zu Hause im Alltagsleben muss alle Sinne des Kindes mit einbeziehen.
Kinder im Vorschulalter gehen mit Einfallsreichtum, Offenheit, Interesse, Neugier und Lernfreude grundlegenden mathematischen Aktivitäten nach.
Vorschulkinder

• vergleichen,
• ordnen,
• sortieren,
• zählen,
• teilen ein,
• erkennen und erfinden Muster.

Diesen natürlichen Zugang zur Mathematik, die Möglichkeit die obigen Tätigkeiten spielerisch einzuüben, finden Kinder normalerweise in ihrer all­täglichen Umwelt.
Eine veränderte Kindheit führt heute jedoch zunehmend zu einer nicht mehr ausreichenden Auseinandersetzung mit Mustern, Strukturen und den obigen Tätigkeiten, die alle zu den grundlegenden mathematischen Vorläuferfähigkeiten gehören.
Der natürli­che Zugang kann aber durch vorbereitete Lernumgebun­gen zu Hause oder in einer außerschulischen Förderung gezielt unterstützt werden.
Dabei werden durch die Anleitung zu einem aktiv handelnden Umgang mit Materialien und
Lerngegenstän­den

• Interessen geweckt,
• Vorerfahrungen vertieft,
• Fragen eröffnet,
• Beziehungen entdeckt,
• Schlussfolgerungen gezogen,
• Voraussagen getroffen.

Schon in der Vorschulzeit können die unterschiedlichen Zahlaspekte über eine spielerische Auseinandersetzung mit mathematischen Inhalten ganzheitlich in fantasievollen Zusam­menhängen über Aktivitäten, Lieder, Geschich­ten, Spiele und Übungen am PC erkun­det werden.
Dabei sollten ...

• abwechslungsreiche Aufgaben das mathematische Denken.
  fördern und fordern,
• die Kinder Freude  an der Auseinandersetzung mit Mathema­tik gewinnen,
• und Erfahrungen mit mathematischen Strukturen sammeln.
   

Um einen die gesamte Schulzeit über tragfähigen Zahlbegriff aufbauen zu können, müssen folgende aufeinander aufbauende Sachstrukturelemente in der Vorschulzeit unbedingt angeleitet gefördert werden:

• Benennen und Verstehen von Eigenschaftskategorien (Form, Größe, Farbe)
• Aufbau einer sicheren Raum-Lage-Orientierung (vor / hinter, über / unter, neben / in / auf , rechts / links)
• Beurteilen von Mächtigkeitsrelationen (größer – kleiner, mehr – weniger – gleich viel)
• Konstanz der Gleichmächtigkeit von Mengen (Invarianz, Repräsentanz)
• Mengen- und Zahlanalyse (Inklusion, Seriation)
• Zahl als Klassenbegriff (Klassifikation)
• Zahl als Beziehungsbegriff (Beziehungszahl-Aspekt)
• Beschäftigung mit geometrischen Strukturen und Begriffen

Die moderne Hirnforschung hat gezeigt, dass das Denken in zwei Bereichen er­folgt, die in unterschiedlichen Teilen des Gehirns lokalisiert sind:

• Der eine Bereich ist auf den regelhaften Umgang mit Zeichen- und Symbolsystemen ausgerichtet, dazu gehören die Zahlensymbole.
• Der andere Bereich befasst sich mit der visuellen Wahrnehmung und  Verarbeitung von Bildern, Linien, Flächen und Körpern im Raum.

In diesen Bereich gehören die geometrischen Formen, aber auch die Vor­stellungsbilder von Anzahlen, wie z.B. die Mengen-Bilder-Bausteine, Wür­fel-Bilder, Finger-Bilder, Strich-Bilder u.a..

Aufgabenbereiche, mit denen die notwendigen Vorläuferfähigkeiten
bis zur Einschulung gezielt angeleitet werden können

 A.     Geometrische Grundvoraussetzungen

1.   Sehen und Vorstellen (Visuelle Wahrnehmung)       
2.   Raumerfahrung und Orientierung
3.   Flächen und Körper
4.  Ziffernschreibkurs als erste geometrische Übung

B.    Grundlegende mathematische Fertigkeiten

1.   Ordnen
2.   Sortieren
3.   Vergleichen

C.   Zählen und Zahlen - Anzahlerfassung

D.    Zerlegbarkeit von Anzahlen

Zusammensetzten und Zerlegen von Zahlen auf der Anzahlbildebene

a.   über den handelnden Umgang mit Anzahlbildkarten
b.   mit Legematerial beim Einrichten der Zahlenwohnungen
c.   über Übungen an einem PC-Programm     
d.   auf Arbeitsblättern

E.     Teil-Teil-Ganzes-Konzept  
         -   Zahlen als gegliederte Quantitäten  -

1.   Einführung in das Teil-Teil-Ganzes-Konzept auf der       Rechentafel
2.   Erstes Arbeiten mit Zahlentripeln

F.    Hinführung zur systematischen Erarbeitung aller Zahlzerlegungen im Zahlenraum bis 10

 Detaillierte Darstellung der Aufgabenbereiche A - F

A.     Geometrische Grundvoraussetzungen

Vielfältige geometrische Erfahrungen sind eine wichtige Grundlage

• für das Zurechtfinden in der eigenen Umgebung und 
• für das mathematische Lernen im Allgemeinen. 

 A1.   Sehen und Vorstellen (Visuelle Wahrnehmung)

• Visuomotorische Koordination (das Sehen mit den Bewegungen des Körpers koordinieren)
• Figur-Grundwahrnehmung (aus einer Vielzahl von Reizen den für die Situation wesentlichen herausfiltern)
• Visuelles Speichern (visuelle Wahrnehmung verinnerlichen und im Gedächtnis verankern)
• Visuelles Operieren (in Gedanken Handlungen mit visuell Wahrgenommenem ausführen, verändern und verallgemeinern können)

 A2.   Raumerfahrung und Orientierung

Die Entwicklung der Raumvorstellung ist ein sehr komplexer Vorgang.
Grundvoraussetzung dafür ist,

• dass das Kind seinen eigenen Körper detailliert wahrnimmt und
• Lagebeziehungen am eigenen Körper erfasst.

Später durchdringt das Kind seine Umwelt durch das Erkennen räumlicher Beziehungen.
Es orientiert sich dabei,

• indem es Gegenstände in Bezug zum eigenen Körper wahrnimmt („Der Ball liegt vor mir.“),
• Gegenstände zueinander in Beziehung setzt  (Der Ball liegt neben dem Tisch.“),
• indem es sich bewusst im Raum bewegt („Ich gehe nach rechts, dann komme ich zu … .“).
• indem es lernt einen Perspektivwechsel vorzunehmen und sodann den Blick aus unterschiedlichen Perspektiven unterscheiden kann. 

A3.   Flächen und Körper

Damit das Kind seine Umwelt nach unterschiedlichen Gesichtspunkten ord­nen, Gemeinsamkeiten und Unterschiede entdecken kann, müssen geometri­sche Begriffe erlernt werden (dick – dünn, lang – kurz, hoch – flach, rund, dreieckig, viereckig u.a.). 

A4.   Ziffernschreibkurs als erste geometrische Übung 

Das Kind lernt zunächst geometrische Formen (Bogen, Ecke, Linie, Haken, …) und Lagebeziehungen (senkrecht, von rechts, nach unten, …) zu beschreiben.
Das Kind muss, um Verwechslungen und damit Fehler durch ungenaue Schreibungen zu vermeiden, eine formklare und seitenrichtige Schreibung der Zahlsymbole 0 - 9 erlernen. 
Darüber hinaus ist es für das Kind notwendig, eine automatisierte und bewegungsökönomische Schreibung zu entwickeln, um nicht durch zu hohe Nach­denkkapazitäten über die Schreibung der Zahlsymbole die allgemeine Auf­merksamkeit zu schmälern. Beim Erlernen der Ziffernschreibung wird der verbindliche Bewegungsablauf zunächst durch das Mitsprechen der Richtungen und Formen bewusst ge­macht und durch Ganzkörperbewegungen zusätzlich im Gehirn verankert.

 B.      Grundlegende mathematische Fähigkeiten

Um sein alltägliches Leben bewältigen zu können, sind für jedes Kind folgende mathematische Fähigkeiten grundlegend wichtig:

• Handlungsabläufe strukturieren können
• Gegenstände nach ihren Eigenschaften klassifizieren können
• Mengen als abstrakte Größen erfassen können
• Mengen hinsichtlich ihrer Anzahl vergleichen können

 B1.   Strukturierung des Denkens (klassifizieren und ordnen)

• Über vergleichende Fragen werden Abhängigkeiten zwischen Begriffen herausgearbeitet.
• Vergleiche und Unterschiede werden über Eigenschaften (Form, Farbe, Größe, Material u.a.) festgemacht.
• Beim Klassifizieren wird eine Beziehung zwischen einem Ober- und einem Unterbegriff hergestellt.

Die Kinder sollen zum Beispiel ...

• aus einer Reihe von Gegenständen ein nicht-passendes Objekt herausfinden und ihre Auswahl begründen können,
• zusammengehörige Objekte gruppieren und den Oberbegriff dazu nennen können.

 B2.   Serialität (sortieren, Reihen und Muster legen)

Erfahrungen zur Serialität sind wichtig beim Aufbau von Zahlenreihen und für das Verstehen von Richtungen und Reihenfolgen in einem Zahlenraum. Sie sind Voraussetzungen, um logische Schlüsse zu ziehen und Wenn-dann-Re­lationen zu verstehen. 

• Kinder müssen das Gefühl für Zeitabläufe erst entwickeln.
• Sie müssen den Ablauf einer Handlung (zuerst – dann – zuletzt) erst erlernen.
• Solche serialen Fähigkeiten sind eine Voraussetzung für die Entwicklung mathematischen Denkens, denn gedachte und auszuführende Handlungen müssen stets der Reihe nach geschehen.

Seriale Fähigkeiten werden erworben und geübt, indem die Kinder ...

• Bilder entsprechend dem Zeitablauf einer Handlung ordnen,
• konkrete Gegenstände nach einem Muster aufreihen,
• Muster und Reihen immer wieder erkennen und fortsetzen üben,Handlungen nach Vorschrift ausführen.      

B3.   Vergleichen

Das Kind erlernt, Objekte nach quantitativen Merkmalen zu vergleichen.
Es soll dabei Begriffe wie „mehr, weniger, gleich viel, am meisten, die we­nigsten …“ zu verwenden lernen.Die Vergleiche sollen durch

• Schätzen,
• Eins-zu-eins-Zuordnung,
• Abzählen

vorgenommen werden können.
Die Kinder lernen Gleichmächtigkeit und Unterschiede zu erkennen und sprachlich darzustellen.
Bis zu einem Unterschied von 3 Elementen lernen sie auch zu benennen, wie viele Elemente mehr die eine Menge hat, und im Umkehrschluss auch zu bestimmen, wie viele Elemente weniger die andere Menge hat.

a.   Eins-zu-eins-Zuordnung

Kinder müssen Mengenvergleiche nichtzählend über eine Eins-zu-eins-Zuordnung herstellen können. Sie müssen dabei einem Objekt der ei­nen Menge genau ein Objekt der anderen Menge zuordnen können. Solche Aufgaben lassen sich  im Alltag vielfältigfinden:

Beispiele:  

• Beim Tischdecken: „Hole genauso viele Teller, wie Stühle am Tische stehen!“
• Sortieren von Schrauben und Muttern: „Lege zu jeder Schraube eine Mutter! Sind es mehr Schrauben als Muttern oder haben wir genauso viele Muttern wie Schrauben?“ 

b.   Verbindung herstellen von Eins-zu-eins-Zuordnungen        mit  Zahlwörtern

c.   Erkennen von Invarianz 

Das Kind muss erkennen lernen, dass die Mächtigkeit einer Menge gleich bleibt, auch wenn sich die räumliche Anordnung oder Ausdeh­nung ändert.
 

Beispiel: 

• Umschütt-Versuche
• mit gleicher Stein-Anzahl verschiedene Muster legen
• Ausdehnung bereits verglichener Elemente ändern (besonders einsichtig bei Luftballons)

 C.   Zählen und Zahlen  /   Anzahlbestimmung

 Eine Anzahl von Objekten kann auf viererlei Weise bestimmt  werden:

1. durch Zählen
2. durch simultane Anzahlerfassung 
3. durch teil-komplexe Anzahlerfassung (Untergliederung in Teilmengen)
4. durch Wiedererkennen abgespeicherter Vorstellungen von Anzahl­bildern 

Zu 1.:   Bei der Förderung der Zählfähigkeit ist die Unterscheidung folgender Bereiche wichtig: 

• Zahlwortreihen
• Zählen von Objekten
• Kardinales Zahlverständnis           

Das Zählen im Sinne des Erfassens der Mächtigkeit (der Anzahl der Ob­jekte) einer Menge erfolgt nach den folgenden 5 Zählprinzipien: 

• Eindeutigkeitsprinzip (Jedem der zu zählenden Elemente/ Objekte einer Menge wird genau ein Zahlwort zugeordnet.)
• Prinzip der stabilen Ordnung (Die Reihe der Zahlwörter hat eine feste Ordnung.)
• Kardinalzahlprinzip (Das zuletzt genannte Zahlwort gibt die Anzahl der Elmente einer Menge an.)
• Abstraktionsprinzip (Es kann jede beliebige Menge gezählt werden. Es kommt nicht auf die Art der Elemente an, die gezählt werden sollen.)
• Prinzip der Irrelevanz der Anordnung (Die Anordnung der zu zählen­den Elemente hat keinen Einfluss auf das Zählergebnis.)

 Die Entwicklung der Zählfähigkeit erfolgt laut Prof. K. Hasemann in 5 auf­einander aufbauenden  Phasen:

 Phase 1   Verbales Zählen

Mit ca. 3 Jahren beginnen die Kinder die Zahlwortreihe wie ein Gedicht aufzusagen, ohne dass ihnen bewusst ist, dass hinter einem Zahlwort auch die Mächtigkeit einer Menge steckt. Daher kann die Zahlwortreihe auf dieser Stufe noch nicht zum Zählen benutzt werden.

 Phase 2   Asynchrones Zählen

Mit etwa 3 ½ - 4 Jahren benutzen die Kinder zwar die Zahlworte in der richti­gen Reihenfolge, sind aber noch nicht in der Lage, auf ein Objekt zu zeigen und das entsprechende Zahlwort dazu zu nennen.
So kommt es vor, dass sie häufig ein Objekt übersehen oder Elemente mehrmals zählen.

 Phase 3   Ordnen der Objekte während des Zählens

Ab ca. 4 ½ Jahren beginnen Kinder die Objekte während des Zählens zu ordnen. Dies geschieht  z.B. dadurch, dass bereits gezählte Objekte zur Seite geschoben werden.

 Phase 4   Resultatives Zählen

Mit ca. 5 Jahren wird den Kindern bewusst, dass ...

• sie beim Zählen mit der Eins beginnen müssen,
• jedes Objekt nur einmal gezählt wird,
• die letztgenannte Zahl die Anzahl der Objekte angibt.

Phase 5   Abkürzendes Zählen

Von 5 ½ - 6 Jahren an erkennen oder bilden Kinder in ungeordneten Mengen von Objekten Strukturen und können von einer beliebigen Zahl aus aufwärts zählen.
Zusätzlich können die meisten Kinder in diesem Alter bereits einfache Rechnungen ausführen.

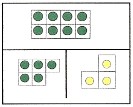
Zu 2.:   Die simultane Anzahlerfassung von bis zu 5 Elementen wird durch das selbstständige Herstellen der vier verschiedenen Anzahlbilder (Mengen-Bilder-Bausteine = MBB, Würfelbilder, Strichbilder und Fingerbilder) mit Legematerial und regelmäßige Blitzblickübungen geschult.

Zu 3.:   Die Anzahlen 6 - 10 lernen die Kinder teilkomplex zu erfassen über die An­zahlbild-Darstellungen in der Form „5 + x“, basierend auf der Kraft der Fünf.

Zu 4.:   Der Aufbau gesicherter Vorstellungsbilder von Anzahlen bis 10 erfolgt durch vielfältige Übungen mit 6 verschiedenen Anzahlbildern (zu den vier un­ter 2. genannten kommen noch die Steckwürfelstangen im Zehnerraster und die Rechenwürfelbilder hinzu). Durch unterschiedlichste Übungen und Spiele mit den „Anzahlbild-Karten“ sowie das eigenständige Herstellen dieser An­zahlbilder mit Legematerial lernen die Kinder zusätzlich auch flexibel mit die­sen Vorstellungsbildern operieren zu können, was eine sichere Vorbeugung gegen das „zählende Rechnen“ ist.

 
D.      Zerlegbarkeit von Anzahlen

Die Kinder erkennen in vielfältigen Spielen mit den Anzahlbildkarten und beim selbstständigen Herstellen der 6 Anzahlbilder mit diversem Legematerial, dass Anzahlen aus Teilmengen zusammengesetzt werden können. 
Die Kinder gelangen dadurch selbst zu der Erkenntnis, dass Anzahlen ...

• andere Anzahlen enthalten,
• in Teilmengen zerlegt werden können und
• aus anderen Anzahlen zusammenzusetzen sind.

Durch die Arbeit mit den 6 verschiedenen Anzahlbildern (Würfelbilder, Strich­bil­der, Fingerbilder , Mengen-Bilder-Bausteinen = MBB, Steckwürfelstangen und Rechenwürfelbilder), bei denen die Darstellungen der Anzahlen 6 - 10 bis auf die MBB alle auf der „Kraft der Fünf“ basieren, erfahren die Kinder zusätz­lich die Anzahlen 6 - 10 als aus 2 Teilmengen zusammengesetzt
( 6 als 5 + 1, 7 als 5 + 2, …).

Beispiele:

• Ein Kind bearbeitet mögliche Zerlegungen des 6ers am PC mit der Soft­ware „ Budenberg Lernprogramme Mathematik“ (Lernprogramm: Mathe 1 > Zerlegen > „Zerlegen 6“)  dabei begleitet es sein Tun z.B. mit den Worten: „Diesen 6er zerlege ich in einen 3er und noch einen 3er! Den nächsten zer­lege ich in einen Einer und einen 5er!“
  
• Beim MBB-Angeln und MBB–Würfeln wird eine bestimmte Anzahl aus kleineren bereits geangelten oder erwürfelten Mengen-Bilder-Bausteinen zu­sammengesetzt.
  Ein Kind benennt beim 5er-Angeln z.B.: 

  „Ich kann aus meinen geangelten MBB vier (unterschiedliche) 5er bauen: einen aus einem 3er und einem 2er, einen aus zwei 2ern und einem Einer, einen aus einem 2er und drei Einern und einen aus fünf Einern.“
  
  Ein Kind probiert beim MBB-Würfeln aus, welche Menge es aus zwei erwür­felten Bausteinen zusammensetzen kann: „Ich habe einen 3er und einen 2er gewürfelt. Mal sehen, was ich daraus bauen kann? Oh, das gibt einen 5er!“ 

• Einrichten der Zahlenwohnungen mit „Möbeln“ 
   „Die Möbel“ sind verschiedene Materialien wie z.B. Hölzchen, Steckwürfel,  Wendeplättchen etc. . Sie werden beim Einrichten jeweils in einer bestimm­ten  Anzahlbildform wie z.B. Strich-Bilder, Würfel-Bilder, MBB-Form usw. ge­legt.
   
  Ein Kind ruft dabei z.B.: „Die Sieben hat für ihr Strich-Bild schon die Holz­stäbchen von der Fünf bekommen. Jetzt fehlen ihr also noch die von der Zwei!“    

E.      Teil-Teil-Ganzes-Konzept  
          -  Zahlen als gegliederte Quantitäten  -
              (von der kardinalen zur relationalen Zahlverwendung)

Die Einführung in das Teil-Teil-Ganzes-Konzept mit der Rechentafel eröffnet den Kindern erste Einsichten in die Zahlbeziehungen.     
Um abstrakte relationale, Beziehungen zwischen Zahlen beschreiben zu kön­nen, wie z. B. „den Unterschied zwischen zwei Zahlen“ bestimmen zu können, muss das Kind zum einen die Zahl als kardinalen Repräsentanten einer Menge verwenden können und zum anderen das Teil-Teil-Ganzes-Konzept verstanden haben.
Wenn das Kind die Mächtigkeit von Zahlen berücksichtigt und die Beziehung zwischen zwei Zahlen erkannt hat, es dann z. B. benennen kann: „Vom 4er zum 6er kommt noch ein 2er dazu!“ (oder „Der 6er hat 2 mehr als der 4er!“), somit auch sagen kann: „Der Unterschied zwischen einem 4er und einem 6er ist ein 2er!“ (später kürzer: „Der Unterschied zwischen 4 und 6 beträgt 2.“), so verwendet es die Zahl 2 relational als Bezeichnung einer Zahlbeziehung.
Wer 4 und 6 nur ordinal als (Haus-) Nummern versteht, ohne sich deren Mächtigkeit bewusst zu sein, würde den Unterschied zwischen zwei Zahlen eher im Aussehen der Zahlsymbole (Ziffern) als in deren Mächtigkeit suchen.
Die Entwicklung des Wissens über Beziehungen zwischen Mengen wird in der mathematikdidaktischen Fachliteratur (Gerster 2003, Resnick 1983, Jansen 2003) als der bedeutsamste Schritt in der Entwicklung des ma­thematischen Verständnisses bewertet. 

• Wenn Kinder verstanden haben, dass Zahlen aus anderen Zahlen zusammengesetzt sind und in unterschiedliche Teilmengen zerlegt werden können, ohne dass man dabei ihre Mächtigkeit verändert (7 = 5 + 2  oder 7 = 3 + 4 oder aber z.B. auch 7 = 6 + 1), wenn sie Zahlen nicht län­ger im Sinne fester quantitativer Einheiten sehen, dann wird es ihnen z.B. auch möglich, das Kommutativgesetz (Tauschaufgaben) zu verstehen (7 = 5 + 2 kann zu 7 = 2 + 5 vertauscht werden) und auch effektive Rechen- bzw. Zerlegungsstrategien wie z.B.  5 + 7 = 5 + 5 + 2 selbstständig anzu­wenden, was u.a. für den verstehenden Umgang mit dem Zehnerübergang unerlässlich ist.
  Diese Erkenntnis, deren Erreichen sich weit in die Grundschulzeit hineinzieht, ermöglicht den Kindern erst einen flexiblen Umgang mit Zahlen beim Lösen von Rechenaufgaben. 
  
• Die spielerische Arbeit mit konkreten Legematerial (Wendeplätt­chen, Holzstäbchen, Steckwürfeln, MBB) auf der Rechentafel ermöglicht den Kindern die Tripel-Struktur von Additions- und Subtraktionsaufgaben zu erkennen.
  
  Alle Additions- und Subtraktionsaufgaben haben eine dreigliedrige (tria­dische) Grundstruktur (Teil-Teil-Ganzes).
  Auf der Rechentafel erkennen die Kinder das Teil-Teil-Ganzes-Konzept von Anzahlen, welches die Beziehungen zwischen den Zahlentripeln spezifiziert.

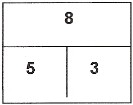	In der Rechentafel steht oben immer das "Ganze" (hier ein "8er") und darunter die beiden "Teile" (hier ein "5er" und ein "3er")		Wenn die Kinder beim "Bauen" von Zerlegungen  mit Mengen-Bilder- Bausteinen angehalten werden, gleich auch die Zahlnamen mit aufzuschreiben, prägen sie  sich schon bei der handelnden Arbeit mit den MBB das dazu- gehörige "Zahlentripel" ein.

Bsp.:   Im Zahlentripel 8 / 5 / 3 ist 8 das Ganze und 5 und 3 sind Teile.

Die Kinder lernen durch das Lösen mit Legematerial auf der Rechentafel von Anfang an, dass diese Teil-Teil-Ganzes-Beziehung bestehen bleibt, egal welche der 24 folgenden Aufgabenstellungen vorgegeben ist.

            5 + 3 = ?       3 + 5 = ?       3 + ? = 8       ? + 5 = 8      
            5 + ? = 8       ? + 3 = 8

                          
Plusaufgaben in bekannter Form mit dem Ergebnis „hinten“ (rechts)

             oder

            ? = 5 + 3      ? = 3 + 5       8 = 3 + ?       8 = ? + 5      
            8 = 5 + ?       8 = ? +3     

ungewohntere Form von Plusaufgaben mit dem Ergebnis „vorne“ (links)

             und

             8 - 5 = ?      8 – 3 = ?        8 - ? = 5        8 - ? = 3       
             ? – 5 = 3        ? – 3 = 5    

Minusaufgaben in bekannter Form mit dem Ergebnis „hinten“ (rechts)

             oder   

             ? = 8 - 5      ? = 8 - 3        5 = 8 - ?        3 = 8 - ?       
             3 = ? - 5        5 = ? - 3

ungewohntere Form von Minusaufgaben mit dem Ergebnis „vorne“

•  Indem von Anfang an Plus- und Minusaufgaben gleichzeitig behan­delt und auf der Rechentafel durch Legen mit Anzahlmaterial gelöst wer­den, entwickelt das Kind schon früh Verständnis für die Tausch- und Umkehr­aufgabenbeziehungen und lernt dabei, aus den 3 Zahlen eines Zahlentripels immer gleich 2 Plus- und 2 Minusaufgaben bilden zu können. (Vielen Schülern, die herkömmlich unterrichtet werden, indem Plus- und Minusaufga­ben zu unterschiedlichen Zeitpunkten eingeführt und bearbeitet werden,  er­scheinen Minusaufgaben häufig viel schwerer als Plusaufgaben da sie selten die Beziehung zwischen beiden erkennen und so z. B. eine „schwere Minus­aufgabe“ auch nicht aus einer ihnen bekannten Plusaufgabe ableiten.)
  
• Werden dann wie oben beschrieben noch Aufgaben mit Leerstellen an allen möglichen Stellen und Aufgabenterme, bei denen das Ergebnis einmal rechts und einmal links vom Gleichheitszeichen steht, vorgegeben und handlungsorientiert mit Legematerial auf der Rechentafel gelöst, so lernt das Kind, Aufgabentypen mit Leerstellen und Aufgaben, bei denen „das Ergebnis vorne steht“ (die den Schülern sonst zumeist sehr schwer fallen), von Anfang an zu verstehen.

Das Kind erwirbt durch das Vorgeben unterschiedlichster Aufgabenstellungen zu ein und demselben Zahlentripel schnell eine für das spätere zügige Kopf­rechnen wichtige operative Flexibilität.
Aufgaben mit unbekannter Anfangsmenge bleiben für Schüler ohne ein Ver­ständnis des Teil-Teil-Ganzes-Zusammenhangs meist unlösbar.

F.      Hinführung zur systematischen Erarbeitung          aller Zahlzerlegungen im Zahlenraum bis 10

Weiterführend können zu Hause alle Zahlzerlegungen der Zahlen bis 10 sys­tematisch erarbeitet werden mit Hilfe des Legematerials „Mengen-Bilder-Bau­steine“ und „Anzahlstangen“ (siehe Band 2: Arbeitsmittel des Grundlagen- und Förderkurses „Freundschaft schließen mit den Zahlen 0 - 10“) und der Ar­beitsblätter zur handelnden Erarbeitung aller Zahlzerlegungen der Zahlen bis 10 über die Rechentafel (siehe Band 3: Arbeitsblätter des Grundlagen- und Förderkurses „Freundschaft schließen mit den Zahlen 0 - 10“).
In den Umgang mit diesen Aufgabenstellungen und Arbeitsblättern werden die Kinder gegen Kursende eingeführt.

Mit dem Material des von mir aus der Praxis heraus entwickelten Grundlagen- und Förderkurses „Freundschaft schließen mit den Zahlen 0 – 10“ können die vorlaufend beschriebenen und ausführlich dargestellten Aufgabenberei­chen A – F in häuslichen Übungen selbst angeleitet mit den Kindern erarbeitet werden.

Fotos aus meinen eigenen Frühförderkursen finden sich unter dem Schlater "Fotos vom Kurs".